Gravitatieconstante

De gravitatieconstante, constante van de zwaartekracht of constante van Cavendish is een natuurkundige constante die in de gravitatiewet van Newton aangeeft hoe de zwaartekracht tussen twee voorwerpen, hun massa's en hun afstand zich verhouden tot elkaar. Het is de natuurconstante, die de sterkte van de zwaartekracht bepaalt.

De gravitatieconstante G in de gravitatiewet van Newton.

In de algemene relativiteitstheorie volgens Albert Einstein bepaalt deze constante de kromming van de vierdimensionale ruimte-tijd. Iets specifieker: in de Einstein-veldvergelijkingen kwantificeert de gravitatieconstante de relatie tussen de geometrie van de ruimtetijd en de energie-impuls tensor.

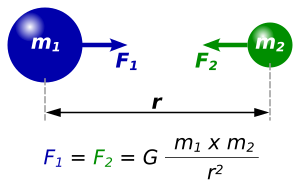
Binnen het SI-stelsel is de constante gelijk aan de kracht in newton die twee objecten met elk een massa van 1 kilogram, op een afstand van 1 meter op elkaar uitoefenen. De constante komt in de gravitatiewet van Newton voor:

$F=G\cdot {\frac {m_{1}\cdot m_{2}}{r^{2}}}$

Daarin is

• $F$ de zwaartekracht tussen twee voorwerpen in newton
• $G$ de gravitatieconstante in m³ s⁻² kg⁻¹ of Nm² kg⁻²
• $m_{1}$ de massa van het eerste voorwerp in kg
• $m_{2}$ de massa van het tweede voorwerp in kg
• $r$ de afstand tussen de middelpunten van de voorwerpen in m

Bepaling

De constante is rechtstreeks te bepalen door middel van het torsiebalans-experiment van Henry Cavendish. Daaruit vond hij een waarde van 6,674 × 10⁻¹¹ m³ s⁻² kg⁻¹.

Toch blijft deze constante een van de minst nauwkeurig bepaalde natuurkundige constanten, met maar drie of vier significante cijfers.

GM-product

Op voldoende grote afstand boven het oppervlak van een zwaar hemellichaam wordt de valversnelling gegeven door:

$g(r)={\frac {GM}{r^{2}}}$

waarin $r$ de afstand tot het middelpunt van het hemellichaam en $M$ de massa van het hemellichaam is.

Inmiddels zijn massa's van hemellichamen op vele verschillende indirecte manieren uit de valversnelling en het GM-product afgeleid: met zonsverduisteringen, de seismologie van de zon, satellietonderzoek, lasers op de Maan, planeetbewegingen en pulsarstatistiek.

Standaardisatie

Er worden door verschillende gezaghebbende instituten verschillende waarden geadviseerd.
De IAU houdt het op

(6,67259 ± 0,00030) × 10⁻¹¹ m³ s⁻² kg⁻¹

Volgens de CODATA-commissie was de beste waarde in 2006

(6,67428 ± 0,00067) × 10⁻¹¹ Nm² kg⁻²

De relatieve onnauwkeurigheid is dus 10⁻⁴ of iets minder.

Wegens de genoemde onnauwkeurigheid was bij de voorgestelde herdefinitie van de basiseenheden de gravitatiewet van Newton niet geschikt voor de herdefinitie van de kilogram. De planckmassa maakt er wel gebruik van. De waarde hiervan in kg heeft dan ook een onnauwkeurigheid die is gerelateerd aan de onnauwkeurigheid in $G$, zij het de helft wegens het nemen van de wortel van $G$.

Bij enkele hemellichamen, waaronder de Zon en de Aarde, is het GM-product met veel grotere nauwkeurigheid bekend dan van $G$ en $M$ afzonderlijk. Voor de Aarde is dit 398 600,4418(9) km³s⁻². De relatieve onnauwkeurigheid is dus 2×10⁻⁹. De relatieve onnauwkeurigheid waarmee de massa van de Aarde bekend is komt dus vrijwel overeen met die van $G$.

Aardmassa

Door de waarde van $G$ in te vullen in de bovenstaande zwaartekrachtswet van Newton kan de massa van de aarde bepaald worden. Met $r$ de reeds bekende straal van de aardbol en de gemakkelijk te meten valversnelling $F/m_{1}$, wordt met $m_{2}$ de massa van de aarde gevonden.

Valversnelling naar de Aarde

Bij een bolsymmetrische Aarde geldt voor een object:

$g={\frac {GM}{r^{2}}}$

Daarin is:

g de valversnelling naar de Aarde in ms⁻²

GM = 3,986 004 418(9)×10¹⁴ m³s⁻²

r de afstand tot het massamiddelpunt van de Aarde in m

De relatieve nauwkeurigheid van de formule voor de werkelijke Aarde is het grootst op grote afstand daarvan. Dichterbij zijn er nauwkeuriger formules die rekening houden met de breedtegraad en de plaatselijke hoogte van het aardoppervlak, en zijn ook zwaartekrachtanomalieën van belang.

Externe links

• (en) Jet Propulsion Laboratory, "Astrodynamic Constants". met de gravitatieconstante
• (en) National Institute of Standards and Technology, "Newtonian constant of gravitation G".